I2I Translation

⚠️ 以下所有内容总结都来自于 大语言模型的能力，如有错误，仅供参考，谨慎使用
🔴 请注意：千万不要用于严肃的学术场景，只能用于论文阅读前的初筛！
💗 如果您觉得我们的项目对您有帮助 ChatPaperFree ，还请您给我们一些鼓励！⭐️ HuggingFace免费体验

2025-06-04 更新

Brain network science modelling of sparse neural networks enables Transformers and LLMs to perform as fully connected

Authors:Yingtao Zhang, Diego Cerretti, Jialin Zhao, Wenjing Wu, Ziheng Liao, Umberto Michieli, Carlo Vittorio Cannistraci

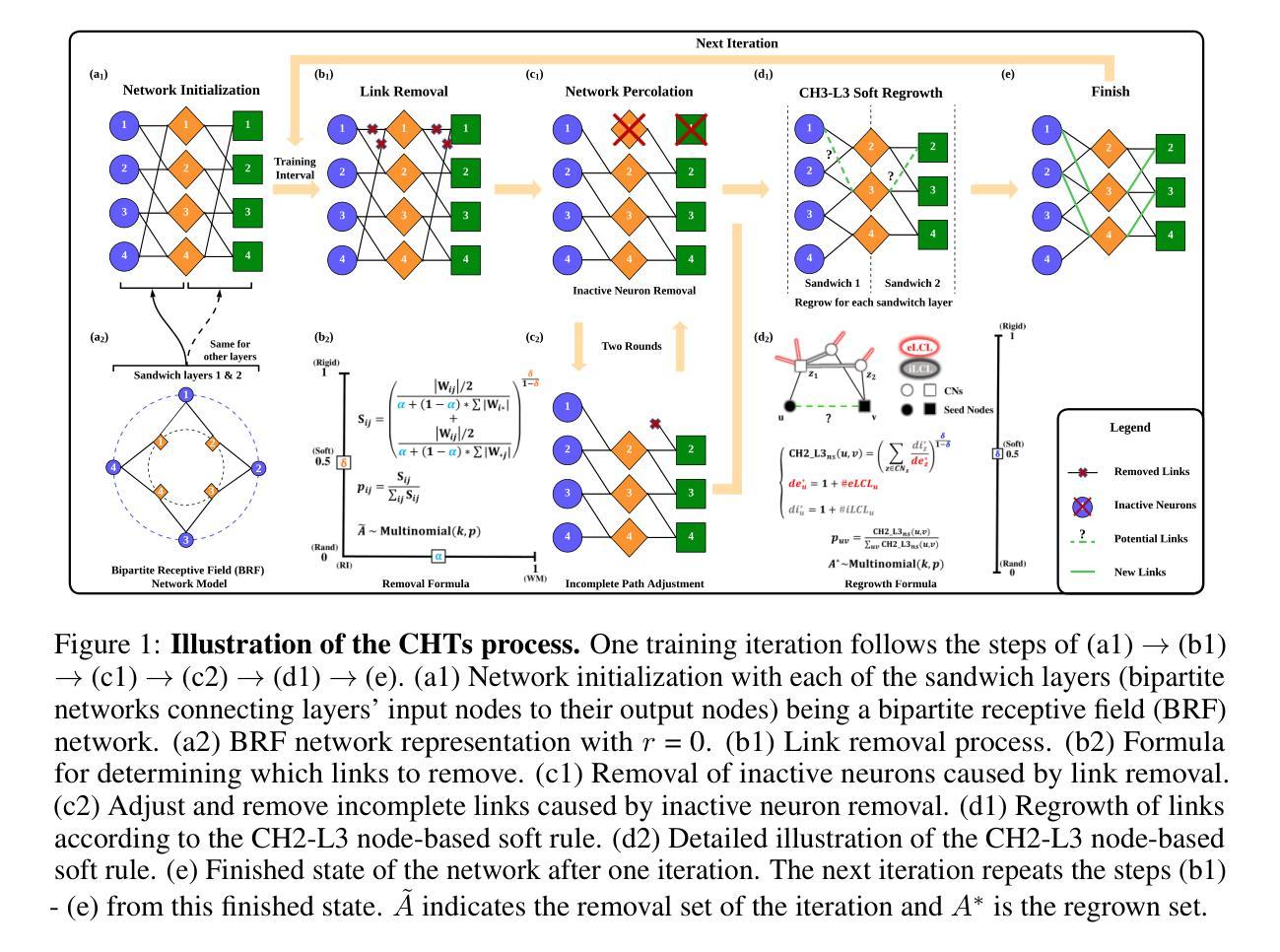
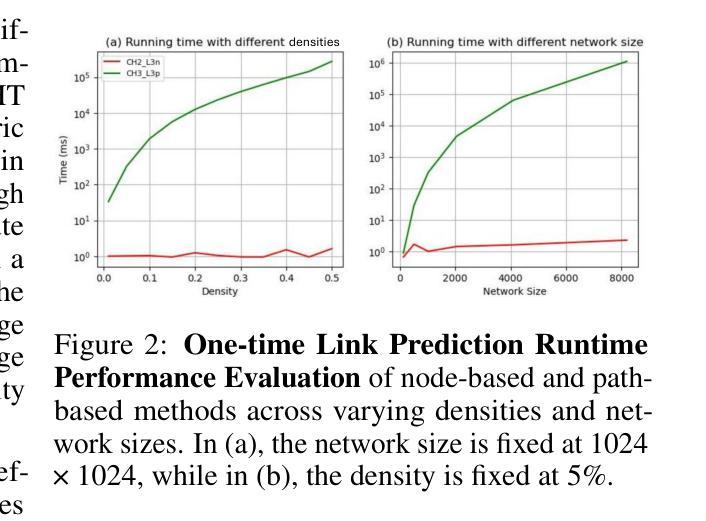
Dynamic sparse training (DST) can reduce the computational demands in ANNs, but faces difficulties in keeping peak performance at high sparsity levels. The Cannistraci-Hebb training (CHT) is a brain-inspired method for growing connectivity in DST. CHT leverages a gradient-free, topology-driven link regrowth, which has shown ultra-sparse (less than 1% connectivity) advantage across various tasks compared to fully connected networks. Yet, CHT suffers two main drawbacks: (i) its time complexity is $O(Nd^3)$ - N node network size, d node degree - restricting it to ultra-sparse regimes. (ii) it selects top link prediction scores, which is inappropriate for the early training epochs, when the network presents unreliable connections. Here, we design the first brain-inspired network model - termed bipartite receptive field (BRF) - to initialize the connectivity of sparse artificial neural networks. We further introduce a GPU-friendly matrix-based approximation of CH link prediction, reducing complexity to $O(N^3)$. We introduce the Cannistraci-Hebb training soft rule (CHTs), which adopts a flexible strategy for sampling connections in both link removal and regrowth, balancing the exploration and exploitation of network topology. Additionally, we integrate CHTs with a sigmoid gradual density decay (CHTss). Empirical results show that BRF offers performance advantages over previous network science models. Using 1% of connections, CHTs outperforms fully connected networks in MLP architectures on image classification tasks, compressing some networks to less than 30% of the nodes. Using 5% of the connections, CHTss outperforms fully connected networks in two Transformer-based machine translation tasks. Finally, at 30% connectivity, both CHTs and CHTss outperform other DST methods in language modeling and even exceed fully connected baselines in zero-shot tasks.

动态稀疏训练（DST）可以减少人工神经网络（ANNs）的计算需求，但在保持高稀疏性时的性能高峰面临困难。Cannistraci-Hebb训练（CHT）是一种受大脑启发的在DST中增加连接性的方法。CHT利用无梯度、拓扑驱动的连接再生，与全连接网络相比，在各种任务中显示出超稀疏（少于1%的连接）的优势。然而，CHT存在两个主要缺点：（i）其时间复杂度为O(Nd^3)（N为节点网络大小，d为节点度），仅限于超稀疏状态。（ii）它选择顶级链接预测分数，这在网络呈现不可靠连接时，对于早期训练周期是不合适的。在这里，我们设计了第一个受大脑启发的网络模型——称为二部接收场（BRF）——来初始化稀疏人工神经网络的连接性。我们进一步引入了CH链接预测的GPU友好矩阵近似方法，将复杂度降低到O(N^3)。我们介绍了Cannistraci-Hebb训练的软规则（CHTs），它采用灵活的采样策略进行链接的删除和再生，平衡网络拓扑的探索与利用。此外，我们将CHTs与Sigmoid逐步密度衰减（CHTss）相结合。经验结果表明，BRF在之前的网络科学模型中表现出性能优势。在仅使用1%的连接情况下，CHTs在多层感知器架构的图像分类任务上优于全连接网络，将某些网络压缩到不到30%的节点。在使用5%的连接情况下，CHTss在基于Transformer的机器翻译任务中优于全连接网络。最后，在30%的连接度下，CHTs和CHTss在语言建模中都优于其他DST方法，甚至在零射击任务中超过了全连接的基线。

论文及项目相关链接

PDF

Summary
动态稀疏训练（DST）能够降低人工神经网络（ANN）的计算需求，但在保持高稀疏性时的性能峰值方面存在挑战。Cannistraci-Hebb训练（CHT）是一种用于在DST中增加连接性的脑启发方法。本文通过引入一种新颖的脑启发网络模型——二分接收场（BRF），对稀疏人工神经网络的连接进行初始化。同时改进了CH链接预测的GPU友好矩阵近似方法，降低了复杂度，并引入了灵活的采样连接策略。实证结果表明，BRF相较于之前的网络科学模型具有性能优势。在仅使用1%的连接时，CHTs在图像分类任务中的多层感知器架构上表现出超越全连接网络的能力，并对某些网络进行节点压缩至30%以下。使用5%的连接时，CHTss在基于Transformer的机器翻译任务中表现优异。最后，在30%的连接率下，CHTs和CHTss在语言建模任务中的表现均优于其他DST方法，并在零样本任务中甚至超过了全连接基线。

Key Takeaways

1. 动态稀疏训练（DST）可降低人工神经网络（ANN）的计算需求，但在高稀疏性时面临性能挑战。
2. Cannistraci-Hebb训练（CHT）是一种脑启发方法，用于在DST中增加网络连接的灵活性。
3. 引入新颖的脑启发网络模型——二分接收场（BRF）进行稀疏人工神经网络的初始化。
4. 改进了CH链接预测的GPU友好矩阵近似方法，降低时间复杂度。
5. CHTs策略采用灵活的采样连接方法，平衡网络拓扑的探索与利用。
6. 在不同连接率下，CHTs和CHTss在多种任务上表现出超越全连接网络的优势。

Cool Papers

点此查看论文截图

Go With the Flow: Fast Diffusion for Gaussian Mixture Models

Authors:George Rapakoulias, Ali Reza Pedram, Fengjiao Liu, Lingjiong Zhu, Panagiotis Tsiotras

Schrodinger Bridges (SBs) are diffusion processes that steer, in finite time, a given initial distribution to another final one while minimizing a suitable cost functional. Although various methods for computing SBs have recently been proposed in the literature, most of these approaches require computationally expensive training schemes, even for solving low-dimensional problems. In this work, we propose an analytic parametrization of a set of feasible policies for steering the distribution of a dynamical system from one Gaussian Mixture Model (GMM) to another. Instead of relying on standard non-convex optimization techniques, the optimal policy within the set can be approximated as the solution of a low-dimensional linear program whose dimension scales linearly with the number of components in each mixture. The proposed method generalizes naturally to more general classes of dynamical systems, such as controllable linear time-varying systems, enabling efficient solutions to multi-marginal momentum SB between GMMs, a challenging distribution interpolation problem. We showcase the potential of this approach in low-to-moderate dimensional problems such as image-to-image translation in the latent space of an autoencoder, learning of cellular dynamics using multi-marginal momentum SB problems, and various other examples. We also test our approach on an Entropic Optimal Transport (EOT) benchmark problem and show that it outperforms state-of-the-art methods in cases where the boundary distributions are mixture models while requiring virtually no training.

薛定谔桥（SBs）是一种扩散过程，能够在有限时间内将给定的初始分布引导到另一个最终分布，同时最小化适当的成本函数。尽管最近在文献中提出了各种计算SB的方法，但即使对于解决低维问题，大多数这些方法也需要计算成本高昂的训练方案。在这项工作中，我们为引导动力系统从一个高斯混合模型（GMM）到另一个GMM的分布，提出了一组可行策略的解析参数化方法。我们并非依赖于标准的非凸优化技术，而是可以将集合内的最佳策略近似为低维线性程序的解，其维度与每个混合中的组件数量呈线性关系。所提出的方法自然地推广到更一般的动力系统类，如可控线性时变系统，为解决GMM之间的多边际动量SB、挑战性的分布内插问题提供了高效解决方案。我们展示了这种方法在低至中等维度的潜力，例如在自动编码器的潜在空间中的图像到图像翻译、使用多边际动量SB问题学习细胞动力学和各种其他示例。我们还对熵最优传输（EOT）基准测试问题进行了测试，结果表明，当边界分布为混合模型时，该方法优于现有技术，并且几乎不需要进行训练。

论文及项目相关链接

PDF

Summary：

本文介绍了Schrodinger桥（SBs）作为一种扩散过程，能够在有限时间内将初始分布引导到最终分布，同时最小化合适的成本函数。尽管最近文献中提出了多种计算SBs的方法，但大多数方法都需要计算昂贵的训练方案，即使对于解决低维问题也是如此。本文提出了一种参数化策略集，用于从高斯混合模型（GMM）引导动态系统的分布。该方法通过低维线性规划来近似最优策略，其维度与混合中组件的数量呈线性关系。该方法可自然地推广到更一般的动态系统类，如可控线性时变系统，并能有效解决多边际动量SB之间的GMM分布插值问题。文章展示了该方法在图像到图像翻译、细胞动力学学习等例子中的潜力，并在Entropic最优传输基准测试中测试了该方法，证明其在边界分布为混合模型的情况下优于现有技术，且几乎无需训练。

Key Takeaways:

1. Schrodinger桥（SBs）是一种扩散过程，用于在有限时间内引导初始分布到最终分布，并最小化成本函数。
2. 现有的计算SBs的方法大多需要昂贵的训练，即使对低维问题也是如此。
3. 本文提出了一种参数化策略集来引导动态系统的分布从高斯混合模型（GMM）到另一个GMM。
4. 该方法通过低维线性规划来近似最优策略，其维度与混合组件的数量线性相关。
5. 该方法适用于更一般的动态系统，如可控线性时变系统，并能解决多边际动量SB之间的GMM分布插值问题。
6. 该方法在图像到图像翻译、学习细胞动力学等实例中表现出潜力。

Cool Papers

点此查看论文截图